The Graham Equity Equation Calculator

This tool uses the mathematical equation proposed by Paul Graham for determining a reasonable portion of equity to offer an employee or investor.

Who is this Paul Graham guy?

Paul Graham is a programmer/entrepreneur from the early days of the internet. He's also one of the co-founders of Y Combinator, and the creator of Hacker News.

How does the Graham Equity Equation work?

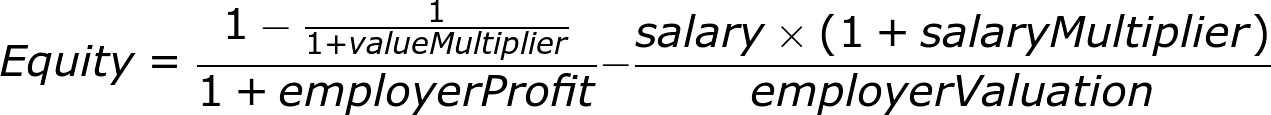
The Graham Equity Equation attempts to determine the amount of equity/salary that would "balance out" the added value that a new employee is expected to bring to a company.

You can read an in-depth explanation of how the equation works in Paul Graham's original blog post here. I'd also recommend this excellent article from Michelle Wetzler, which provides a walkthorugh of three different methods she used to evaluate her own job offer. Her article is especially helpful because - in addition to covering the Graham Equity Equation - it also explores two alternatives for determining compensation.

Can you walk me through an example?

Sure!

Imagine that you're a mid-level embedded software programmer, and you've been offered a spot as the 5th employee at a small, early-stage startup. The startup hasn't received series-A funding, but early seed investments have put their valuation at $10 million. You think that's optimistic, but plausible. After reviewing your budget, you decide that you need $60k/year to live comfortably, and past that you'd like all your compensation to come in the form of equity.

The last thing you need to decide is your "valuation multiplier." On the one hand, you're an early employee, and embedded programmers are hard to come by. On the other hand, you're not a senior-level programmer yet, and you don't have experience designing firmware for the kind of hardware that this startup will be manufacturing. So, you finally decide that adding you to the team will make the company appear roughly 10% more valuable to investors.

Now you're ready to use the Graham Equity Equation to calculate how much equity you should be offered! Click this button to fill the calculator with the for this hypothetical embedded software developer.

What are some shortcomings of the Equity Equation?

The Graham Equity Equation doesn't account for the "market rate" of a particular type of employee. For example, let's say you run a restaurant worth $1mln. You realize that by hiring a delivery driver, you can raise the value of your restaurant by 30%, due to added revenue from delivery orders.

The Equity Equation would tell you that this delivery driver should get an annual salary of $102,000 (assuming you gave him no equity). In reality, however, $102k is well above the $27k average salary for a delivery driver. Paying above the market rate probably makes sense for such a key role, but $102k is pretty far out.

I recommend this article by Michelle Wetzler, in which she takes you through three different methods she used to evaluate her own job offer, only one of which is the Graham Equity Equation.

The equation involves the 4 variables below. By providing any 3 of these numbers, you can solve for the 4th number.

Which number would you like to calculate?


EQUITY

What's this?
The percentage of the company that will/should be given to the new employee.
%

Got it! Now, fill in the other three numbers and hit "calculate."

Hit "Calculate!" to update this number.

ANNUAL SALARY

What's this?
The amount of cash you (or your new hire) will be paid annually.
$

Got it! Now, fill in the other three numbers and hit "calculate."

Hit "Calculate!" to update this number.

VALUATION OF COMPANY

What's this?
How much money the company is currently worth.
$

Got it! Now, fill in the other three numbers and hit "calculate."

Hit "Calculate!" to update this number.

THE NEW HIRE'S "VALUATION MULTIPLIER"

What's this?
By what percentage will the company's valuation increase due to hiring this person? Click here for more.

It can be hard to come up with this number. Think of it this way: startups only hire new people if they believe that adding them to the team will make the company more valuable. Every new hire brings something to the table - maybe they're a great engineer who will help them build a great product, or a really persuasive marketer who will help them boost sales, or an awesome janitor who will make the office a wonderfully clean place to work. Their labor is worth something, and the company will be better off for hiring them.

For this number, try to guess how much better off they will be, as a percentage. If the new hire has some skills that are especially valuable and rare, or if they're joining a very small team, this number may be on the higher end - perhaps 10-30%. Otherwise, common numbers are 1% or 5%.

Another way to think of this: by adding you to the team, about how much more valuable will the company appear to investors?

Ultimately this is a guesstimate, but don't be modest!

Click here to collapse this text.
%

Got it! Now, fill in the other three numbers and hit "calculate."

Hit "Calculate!" to update this number.


The calculator gave me a negative number. What does that mean?

If the calculator computes a negative number for equity, salary, or company valuation, it's essentially telling you that the company will lose money on this hire. For example, if the calculator computes a negative number for equity, it's telling you that the employee should not receive any equity, because the salary you specified is already more than this employee deserves.

In that case, to justify their hiring, the employee should either take a lower salary, or they need to bring more value to the company (which would be reflected in the equation as a higher valuation multiplier). You could also try reducing the "salary multiplier" or "company's profit" advanced parameters.

Likewise, if the calculator computes a negative number for salary, it's telling you that the employee is already being paid more than they're worth in equity, and they would effectively need to pay money to the company to justify getting that equity.

Getting a negative number for the company valuation means something a little different. It specifically means that the employee is being given too much equity - more than their valuation multiplier could ever justify, no matter how valuable the company is.


Advanced Parameters (optional)

The "salary multiplier" and "company's profit" parameters are important inputs in the equation. I’m using Paul Graham’s example values by default, but feel free to tweak them. If you come to regret your tinkering, click here to reset these back to their defaults.

Salary Multiplier (optional)

%

The employee's annual salary is increased by this percentage for the purpose of the equation. This is because an employee’s salary is paid every year, not just once. In addition, the company will incur additional “overhead” costs from the new hire. The salary multiplier accounts for those extra costs.

Company's Profit (optional)

%

If you set this to zero, the Graham Equation would tell you how much equity/salary an employee should receive in order to leave the company neither any better nor worse-off than they were before they hired him/her. When you don’t account for profit, the Graham Equation calculates the “break even” number. No company is interested in merely breaking even on a new hire, so this parameter specifies how much profit they want to make on their new employee.

Howdy!

I'm Steve Trambert. The Graham Equation was helpful to me in negotiating my last job offer, and I hope you find it similarly useful!

I built this tool while teaching myself javascript and HTML/CSS, so if you have any feedback, I'd love to hear from you. Feel free to send me suggestions, friendly criticism, questions, or death threats at grahamEquation@trambert.com.

I don't accept donations myself, but if you found this page helpful and you want to make my day, I'd be very grateful if you would make a donation to my favorite charity, GiveDirectly. GiveDirectly is a lean organization working on a relatively novel approach to international charity, experimenting with direct cash-transfers to low-income individuals. You can find their donation page here, or you can listen to an episode of the Planet Money podcast covering their work here.